Entendendo a importância e conhecendo as características e notações utilizadas nos conjuntos matemáticos
Os conjuntos fazem parte do conhecimento básico da matemática, visto que seu conceito é bastante utilizado em nosso dia a dia.
Assim, é fundamental aprendermos o que eles são e qual tipo de notação utilizam.
Vamos aprender tudo sobre conjuntos?
O que são conjuntos?
Um conjunto representa muito mais uma tipo de noção do que uma definição propriamente dia.
Para sabermos o que é um conjunto, devemos pensar nele como um agrupamento de qualquer quantidade de coisas ou objetos.
Exemplos:
1 – Conjunto dos times campeões brasileiros da série A de futebol
2 – Conjunto dos dias da semanas
3 – Conjunto dos números pares
4 – Conjunto das cores da bandeira do Brasil
Elemento de um conjunto
Um elemento é um item participante de um conjunto. É qualquer uma das coisas ou itens que compõem um conjunto.
Exemplos:
1 – O time do São Paulo é um dos elementes que pertencem ao conjunto dos times campeões brasileiros da série A de futebol
2 – O time do Ceará NÃO é um dos elementes que pertencem ao conjunto dos times campeões brasileiros da série A de futebol
3 – A segunda-feira é um dos elementos que pertencem ao conjunto dos dias da semanas
4 – O numeral 2 pertence ao conjunto dos números pares
5 – O numeral 5 NÃO pertence ao conjunto dos números pares
Tipos de representação dos conjuntos
Devido à sua ideia de agrupamento, é necessário sabermos como representá-los para podermos estudá-los mais facilmente.
Assim, conheça as três principais representações.
1 – Representação tabular
Nessa representação, os conjuntos serão identificados por letras maiúsculas e os elementos ficarão entre chaves separados por vírgulas.
Exemplos
1 – Conjunto dos dias da semana
S = {domingo, segunda, terça, quarta, quinta, sexta, sábado}
2 – Conjunto dos números pares
P = {0, 2, 4, 6,…}
2 – Representação Por propriedades dos elementos
Aqui o conjunto está entre chaves, baseado em uma propriedade comum a todos os seus elementos.
Quando encontramos a seguinte estrutura “x | x” , deve-se ler do seguinte modo: “x tal que x, onde x deve satisfazer a seguinte condição: ”
1 – A = { x | x é dia da semana}
x tal que x deve satisfazer a seguinte condição: x deve ser um dia da semana
2 – B = { y | y é mês do ano}
y tal que y deve satisfazer a seguinte condição: y deve ser um mês do ano
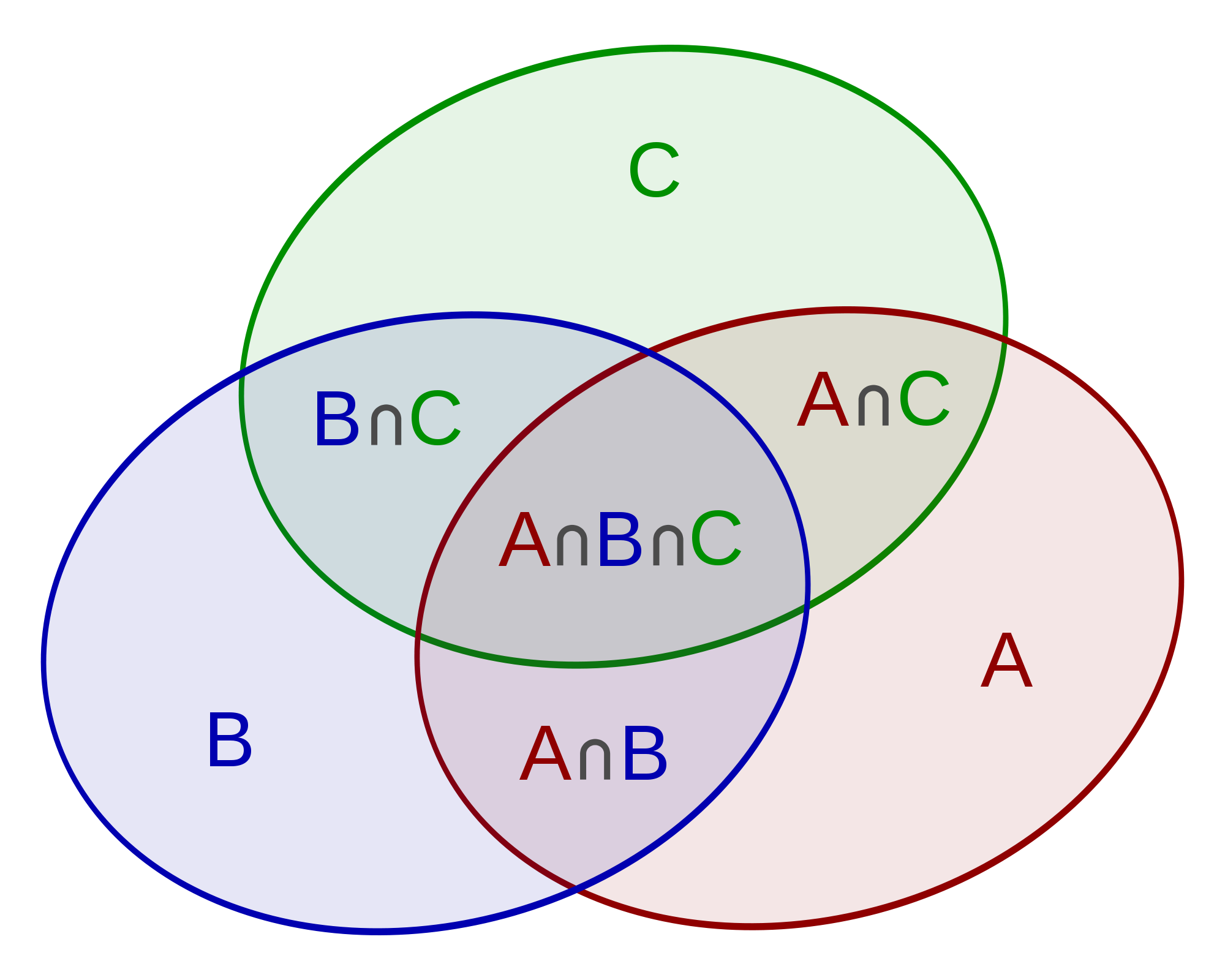
3 – Diagrama de Venn
É uma representação por meio de uma linha fechada e não entrelaçada onde os pontos dentro da linha fechada indicam os elementos do conjunto.
Exemplo do diagrama de Venn:
Tipos de conjuntos
Existem 4 tipos de conjuntos:
1 – Conjunto Finito
Possui um determinado número de elementos de elementos.
Exemplo:
Conjunto dos meses do ano.
A = {janeiro, fevereio, março, abril, maio, junho, julho, agosto, setembro, outubro, novembro, dezembro}
2 – Conjunto Infinito
Não se pode determinar a quantidade de elementos.
Exemplo:
Conjunto dos números naturais.
N = {0, 1, 2, 3, ….}
3 – Conjunto Unitário
Possui um único elemento.
Exemplo: conjuntos dos números pares e primos.
A = {2}
4 – Conjunto vazio
Não possui elementos
Exemplo: conjunto dos números primos pares maiores que dois.
A = {}
Observação: um conjunto vazio pode ser representado por duas formas:
Relação entre elementos e conjuntos
Existe uma notação que relaciona elementos e conjuntos:
Exemplo:
Seja A o conjunto dos estados da região nordeste.
A = { Alagoas, Bahia, Ceará, Maranhão, Paraíba, Piauí, Pernambuco, Rio Grande do Norte , Sergipe}
Assim:
Ceará pertence a A
São Paulo não pertence a A
Relação entre conjuntos
A seguinte notação serve pra relacionar um conjunto com outro conjunto:
Exemplo:
Sejam:
B o conjunto dos estados do Brasil.
A = { Acre, Roraima, São Paulo, Rio de Janeiro, Minas Gerais, Rio Grande do Sul, Goiás, Alagoas, Bahia, Ceará, Maranhão, Paraíba, Piauí, Pernambuco, Rio Grande do Norte , Sergipe,…}
B o conjunto dos estados do nordeste do Brasil.
B = { Alagoas, Bahia, Ceará, Maranhão, Paraíba, Piauí, Pernambuco, Rio Grande do Norte , Sergipe}
C o conjunto dos países europeus
C = {Alemanha, Suécia, Inglaterra, ….}
Assim:
1. B está contido em A
2. A contém B
3. C não está contido em A
4. A não contém C
Subconjuntos
Sejam N e M dois conjuntos. Dizemos que N é subconjunto de M se, e somente se, N está contido em M .
Assim, no exemplo anterior o conjunto dos estados do nordeste é subconjunto do conjunto dos estados do Brasil.
Dica: o conjunto vazio é o menor subconjunto de qualquer conjunto e o próprio conjunto é o maior subconjunto de um conjunto.
Igualdade de conjuntos
Ocorre quando os elementos dos conjuntos sao iguais, independente da ordem.
Exemplo
A = {1, 2, 3}
B = {3, 2, 1}
Logo, A = B
Operações com conjuntos
Existem 3 operações básicas nos conjuntos:
1 – União de conjuntos
Considerando M e N dois conjuntos, a união entre eles é o conjunto formado por elementos de N ou por elementos de M.
Assim,
Exemplo:
2 – Intersecção de conjuntos
Sendo M e N dois conjuntos, a intersecção entre eles é o conjunto formado por elementos que estão em M e N ao mesmo tempo.
Assim,
Exemplo:
3 – Diferença de conjuntos
Sendo M e N dois conjuntos, a diferença entre eles é o conjunto formado pelos elementos que estão em M e não estejam em N.
Assim,
Conclusão
Embora o assunto conjuntos seja básico, existe basante teoria a ser estudada. Aprendemos os diversos tipos de conjuntos, notações e operações envolvida entre eles.
Bons estudos e sucesso!
P.S. Quer aprender um pouco de geometria também? Conheça o teorema de Tales.
Referências
Blog Viche
Brasil Escola