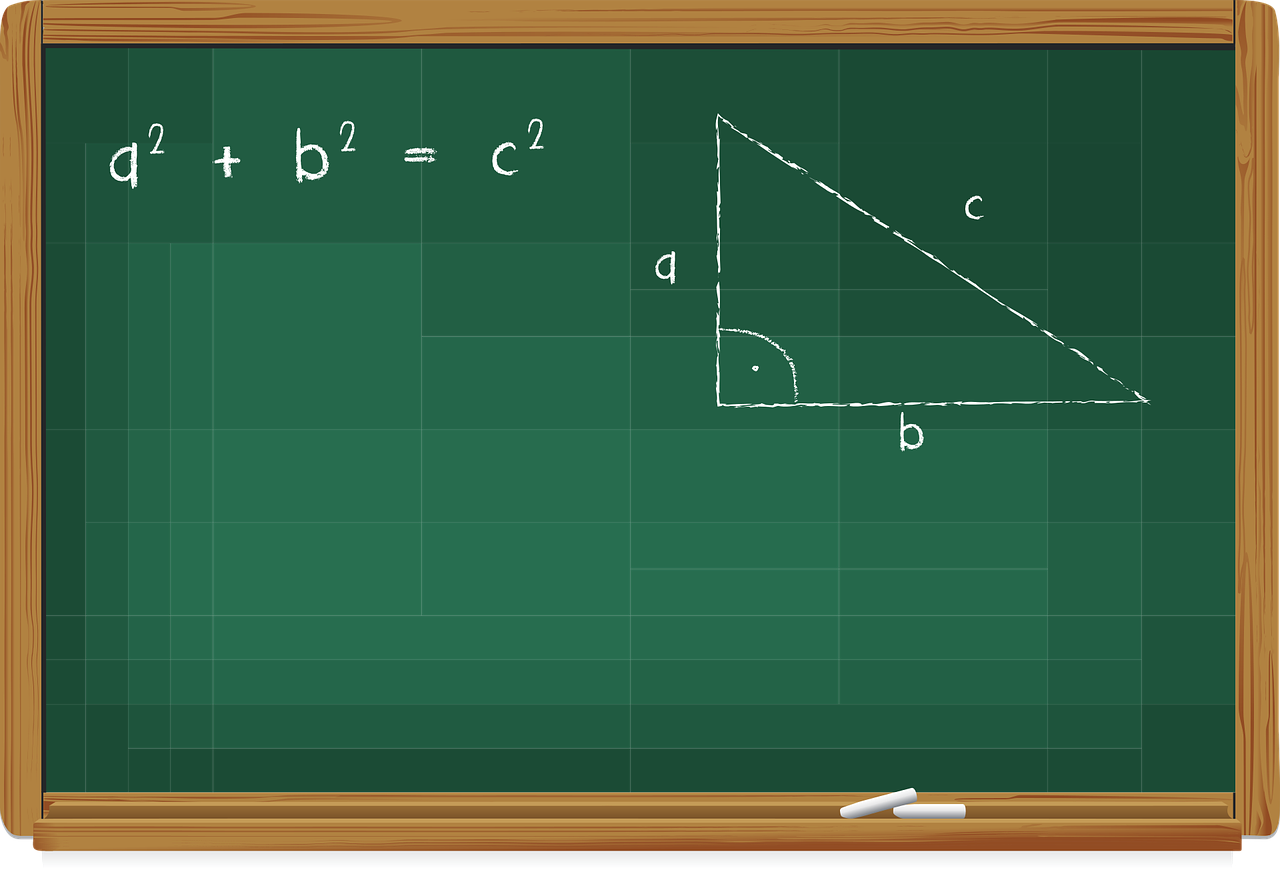
Importância em aprender o Teorema de Pitágoras
O Teorema de Pitágoras é uma das relações mais conhecidas na geometria. Qualquer estudante do ensino fundamental ou médio já ouviu falar de catetos, hipotenusas e sua relação com o Teorema de Pitágoras.
Assim, é fundamental conhecermos bem esse teorema bastante útil.
Relação entre triângulo e quadrados
O teorema de Pitágoras é decorrente de uma relação entre os lados de um triângulo retângulo e as áreas dos quadrados.
Antes de aprofundarmos no assunto, temos alguns conceitos sobre essas figuras geométricas:
1 – Triângulo retângulo: é um triângulo que possui um ângulo de 90º.
2 – Quadrado: quadrilátero que possui todos os lados iguais e todos os 4 ângulos com 90º.
Assim, ao juntarmos três quadrados, teremos o espaço relativo a um triângulo retângulo entre eles:
Pitágoras relacionou então a área formada pelos três quadrados com os lados do triângulo, onde o quadrado da área do quadrilátero oposto ao ângulo de 90º é igual a soma dos quadrados das outras duas áreas:
O triângulo de Pitágoras
Os lados do trîangulo retângulo possuem as seguintes denominações:
Hipotenusa: lado oposto ao ângulo de 90º.
Catetos: demais lados.
O Teorema de Pitágoras
O teorema diz que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
Prática 1
Calcule o valor de X na hipotenusa do triângulo abaixo.
Resolução
O valor de x está representado pela hipotenusa. E um cateto possui o valor 8 e o outro cateto possui o valor 6.
Aplicando o teorema:
Prática 2
Calcule o valor de x no cateto do triângulo abaixo.
Resolução
O valor de x está representado por um dos catetos. Temos a hipotenusa que é 26 e o outro cateto que é 24.
Conclusão
O teorema estuado é aplicado na resoluções de questões envolvendo não apenas matemática, mas também na física e outras disciplinas. Embora seja simples de entender, sua utilidade é basante ampla e serve de base para muitos outros teoremas.
Bons estudos e sucesso.
Que tal aprender um pouco mais de matemática e saber como calcular o vértice de uma parábola?
Referências
Wikipedia