Calculando os volumes dos sólidos geométricos
Depois de aprendermos a calcular ás áreas das principais figuras planas chegou o momento de aprendermos a calcular os volumes dos sólidos geométricos.
Aprenda a calcular os volumes de prismas, cubos, esferas e muitos mais.
Vamos lá?
1. Paralelepípedo retângulo
No paralelepípedo retângulo, o volume é calculado pelo produto da área da base pela altura, conforme visto abaixo:
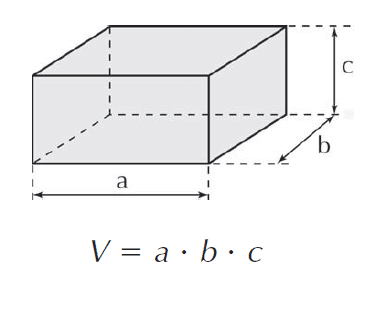
Exemplo
Calcule o volume de um paralelepípedo retângulo, considerando que os lados de sua base medem, respectivamente 5 cm e 8 cm, e sua altura é de 10 cm.
a = 5
b = 8
c = 10
V = a X b X c = 5 X 8 X 10 = 40 X 10= 400 cm3
2. Cubo
Como o cubo possui todas as arestas com medidas iguais, seu volume é calculado pelo produto de sua área de base pela altura. Sendo a área da base igual a a2 e sua altura igual a a, então seu volume é calculado pela expressão a2 X a, originando o volume igual a a3.
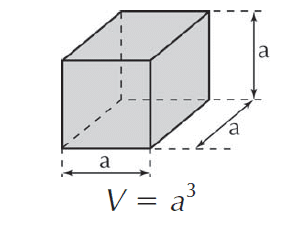
Exemplo
Sendo um cubo com arestas medindo 3 cm, calcule seu volume.
a = 3
V = a3 = 33 = 3 X 3 X 3 = 9 X 3 = 27
3. Prisma regular
Um prisma regular tem sua base formada por lados iguais. Seu volume é calculado pelo produto de sua área da base pela altura.
Exemplo
Um prisma regular tem a área de sua base medindo 20 cm2 e altura medindo 7 cm. Qual seu volume?
B = 20
a = 7
V = B X a = 20 X 7 = 140 cm3
4. Pirâmide
O volume de uma pirâmide é calculado por um terço do produto da área de sua base pela altura.
Exemplo
Temos uma pirâmide com a área de sua base medindo 16 cm2 e sua altura medindo 8 cm. Calcule o volume.
B = 16 cm2
a = 8 cm
V = B X a = 16 X 8 = 128 cm3
5. Cilindro
Normalmente o volume de um sólido é calculado pelo produto da área da base pela altura. Como a base de um cilindro é uma circunferência, cuja área mede πR2 e sua altura mede a, então seu volume é πR2a
Exemplo
Seja um cilindro de base de raio 10 cm e altura igual a 10 cm, calcule seu volume. Considere π = 3,14.
R = 10 cm
a = 10 cm
π = 3,14
V = πR2a = 3,14 X 10 X 10 X 10 = 31,4 X 100 = 3140 cm3
6. Cone
No cone, o volume é calculado por um terço do produto de sua área da base pela altura.
Seja um cone com base de raio igual a 10 e altura igual a 9 cm. Calcule o volume, considerando π = 3,14.
R = 10
a = 9 cm
π = 3,14
V = (3,14 X 102 X 9 )/3= ( 314 X 9 ) / 3 = 314 X 3 = 942 cm3
7. Esfera
Para uma esfera, o volume é calculado da seguinte maneira.
Exemplo
Uma esfera possui raio igual a 3 cm. Calcule seu volume.
R = 3
π = 3,14
V = 4/3 X (π X R3) = (4 X 3,14 X 3sup>3)/3 = = 4 X 3,14 X 27 /3 = 4 X 3,14 X 9 = 113,04 cm3
Conclusão
Nesse artigo aprendemos a calcular os volumes dos sólidos geométricos.
Conhecemos as fórmulas dos volumes dos paralelepípedos, dos cubos, dos prismas, das esferas entre outros.
Vimos diversos exemplos e gravuras representativas.
Até o próximo artigo!
Sucesso e bons estudos!
DICA CASA DA MATEMÁTICA
Aprenda com o Monografis a fazer seu TCC com escrita à prova de plágio sem se preocupar com normas ABNT, seguindo um roteiro já aprovado e ainda receber elogios de familiares e amigos.
Junte-se aos mais de 10 mil alunos do Monografis que tiveram êxito em seus trabalhos de conclusão
O Monografis possui acesso vitalício, online e acessível a partir de qualquer dispositivo.
Além disso, o curso tem compra segura e garantia de 30 dias. E agora com a facilidade de parcelar em até 12x.
Venha conferir o Monografis, o orientador de TCC, e conquistar a aprovação de sua monografia e trabalho de conclusão de curso.
